Category: Computational Imaging

PI Alin Achim

Generalized-Gaussian-Rician Model for SAR Images

Posted on by o.karakus

In this project, we present a novel statistical model, the generalized-Gaussian-Rician (GG-Rician) distribution, for the characterization of synthetic aperture radar (SAR) images. Since accurate statistical models lead to better results in applications such as target tracking, classification, or despeckling, characterizing SAR images of various scenes including urban, sea surface, or agricultural, is essential. In various SAR scenes, the illuminated area may include one (or a small number of) dominating scatterer(s), and a large number of non-dominant ones. Hence, the in-phase and quadrature components of the back-scattered SAR signal become statistically iid, but non-zero-mean random variables.

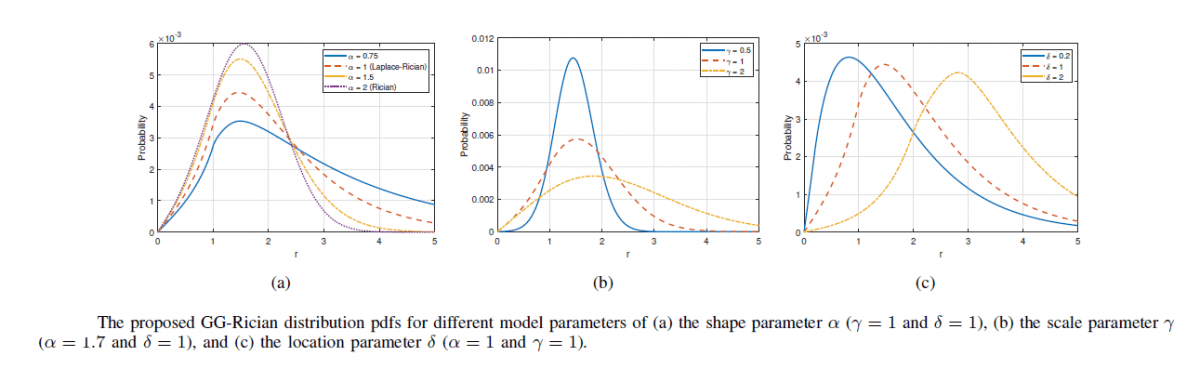
No dominating scatterer (Rayleigh case)
Hybrid case (Rician case)

This idea motivates us to utilise Rician distribution whilst modelling the SAR amplitude. Therefore, the proposed statistical model is based on the Rician distribution to model the amplitude of a complex SAR signal, the in-phase and quadrature components of which are assumed to be generalized-Gaussian distributed.

The GG-Rician statistical model is a general statistical model, which covers various important amplitude and intensity statistical models as special members.

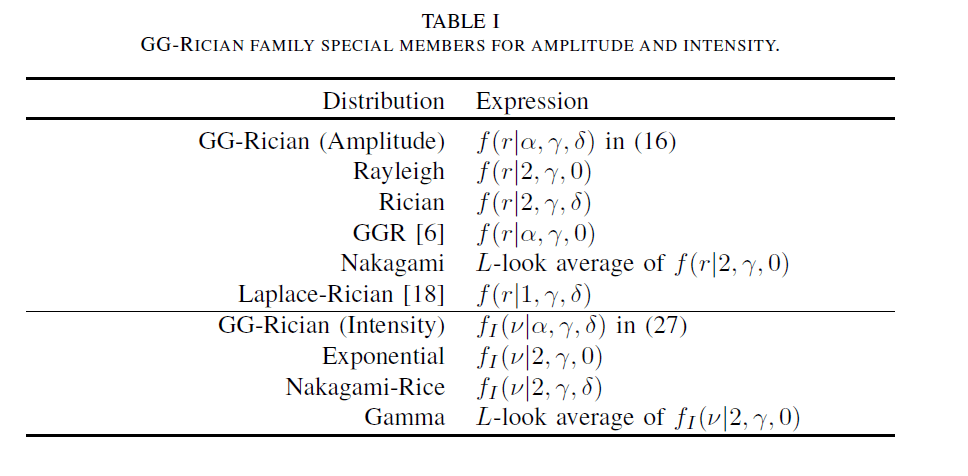
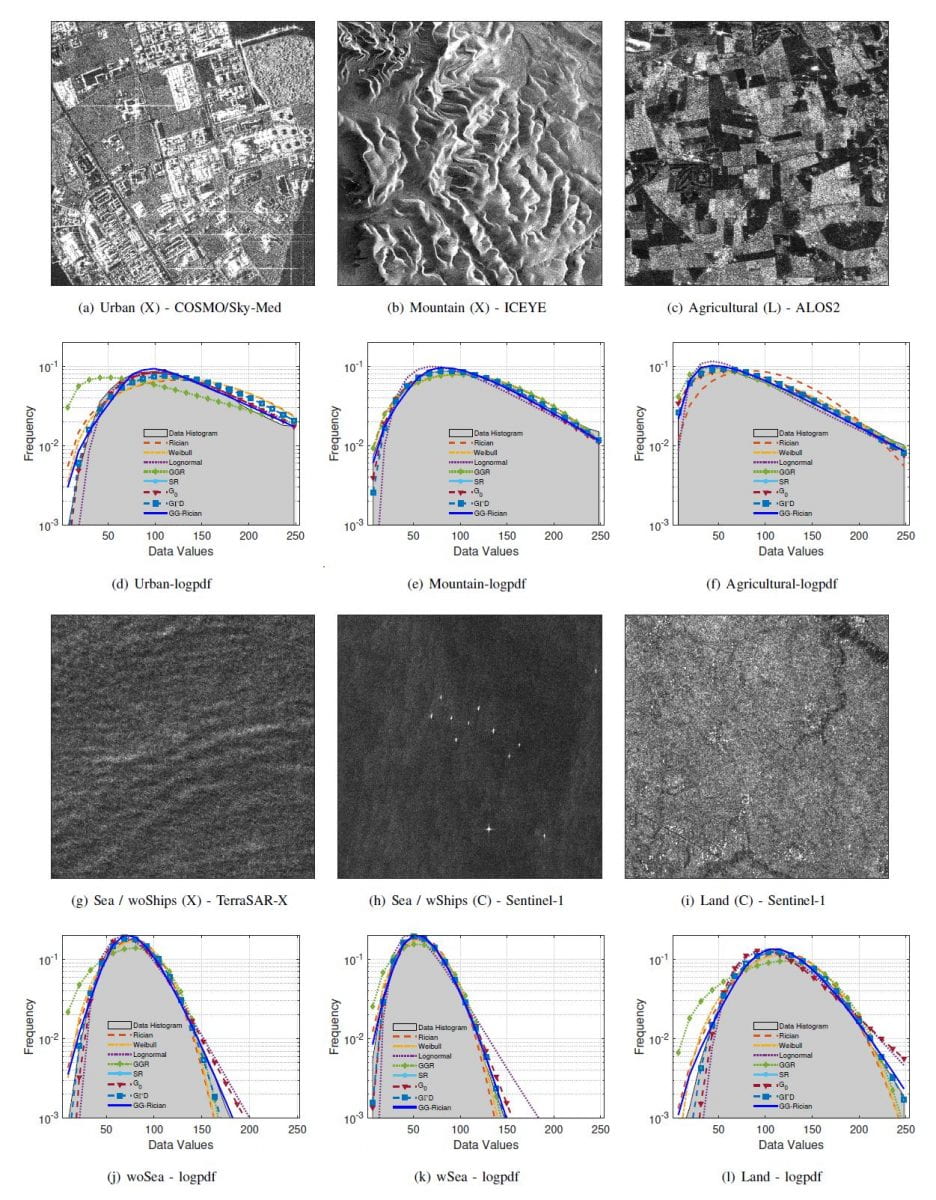
The proposed amplitude GG-Rician model is further extended to cover the intensity SAR signals. In the experimental analysis, the GG-Rician model is investigated for amplitude and intensity SAR images of various frequency bands and scenes in comparison to state-of-the-art statistical models that include

Weibull, G0, Generalized gamma, and the lognormal distribution.

The statistical significance analysis and goodness of fit test results demonstrate the superior performance and flexibility of the proposed model for all frequency bands and scenes, and its applicability on both amplitude and intensity SAR images.

Further information

[1] Karakuş, O., Kuruoglu, E. E., & Achim, A. (2020). A Generalized Gaussian Extension to the Rician Distribution for SAR Image Modeling. arXiv preprint arXiv:2006.08300.

[2] Karakuş, O., Kuruoğlu, E. E., & Achim, A. (2020, May). Modelling sea clutter in SAR images using Laplace-Rician distribution. In ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (pp. 1454-1458). IEEE.

[3] Karakuş, O., Kuruoglu, E. E., & Achim, A. (2020). A Modification of Rician Distribution for SAR Image Modelling.

Contact

Oktay Karakuş, Ercan E. Kuruoglu, Alin Achim

Funding

This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) under grant EP/R009260/1 (AssenSAR).

Cauchy Proximal Splitting (CPS)

Posted on by o.karakus

In this project, we develop a proximal splitting methodology with a non-convex penalty function based on the heavy-tailed Cauchy distribution. We first suggest a closed-form expression for calculating the proximal operator of the Cauchy prior, which then makes it applicable in generic proximal splitting algorithms. We further derive the condition required for guaranteed convergence to the global minimum in optimisation problems involving the Cauchy based penalty function. Setting the system parameters by satisfying the proposed condition ensures convergence even though the overall cost function is non-convex when minimisation is performed via a proximal splitting algorithm.

The proposed proximal splitting method based on Cauchy regularisation is evaluated by solving generic signal processing examples,
** 1D signal denoising in the frequency domain,
** Two image reconstruction tasks including de-blurring and denoising,
** Error recovery in a multiple-antenna communication system.

We experimentally verify the proposed convergence conditions for various cases, and show the effectiveness of the proposed Cauchy based non-convex penalty function over state-of-the-art penalty functions such as L1 and total variation (TV) norms.

Further information

[1] O. Karakuş, P. Mayo and A. Achim, “Convergence Guarantees for Non-Convex Optimisation With Cauchy-Based Penalties,” in IEEE Transactions on Signal Processing, vol. 68, pp. 6159-6170, 2020, doi: 10.1109/TSP.2020.3032231.

Code

O Karakus, A Achim. (2020): Cauchy Proximal Splitting (CPS).
https://doi.org/10.5523/bris.15y437loa26cr2nx8gnn3l4hzi

Contact

Oktay Karakuş, Perla Mayo, Alin Achim

Funding

This work was supported
** in part by the UK Engineering and Physical Sciences Research Council (EPSRC) under grant EP/R009260/1 (AssenSAR),
** in part by a CONACyT PhD studentship under grant 461322 to Mayo,
** in part by a Leverhulme Trust Research Fellowship to Achim (INFHER).