
In this project, we investigate solutions to a number of inverse problems encountered in SAR imaging. We propose a convex proximal splitting method for the optimization of a cost function that includes a non-convex Cauchy-based penalty. The convergence of the overall cost function optimization is ensured through the careful selection of model parameters within a forward-backwards (FB) algorithm. The performance of the proposed penalty function is evaluated by solving three standard SAR imaging inverse problems, including
** Super-resolution,
** Image formation,
** Despeckling,
** Ship wake detection for maritime applications.
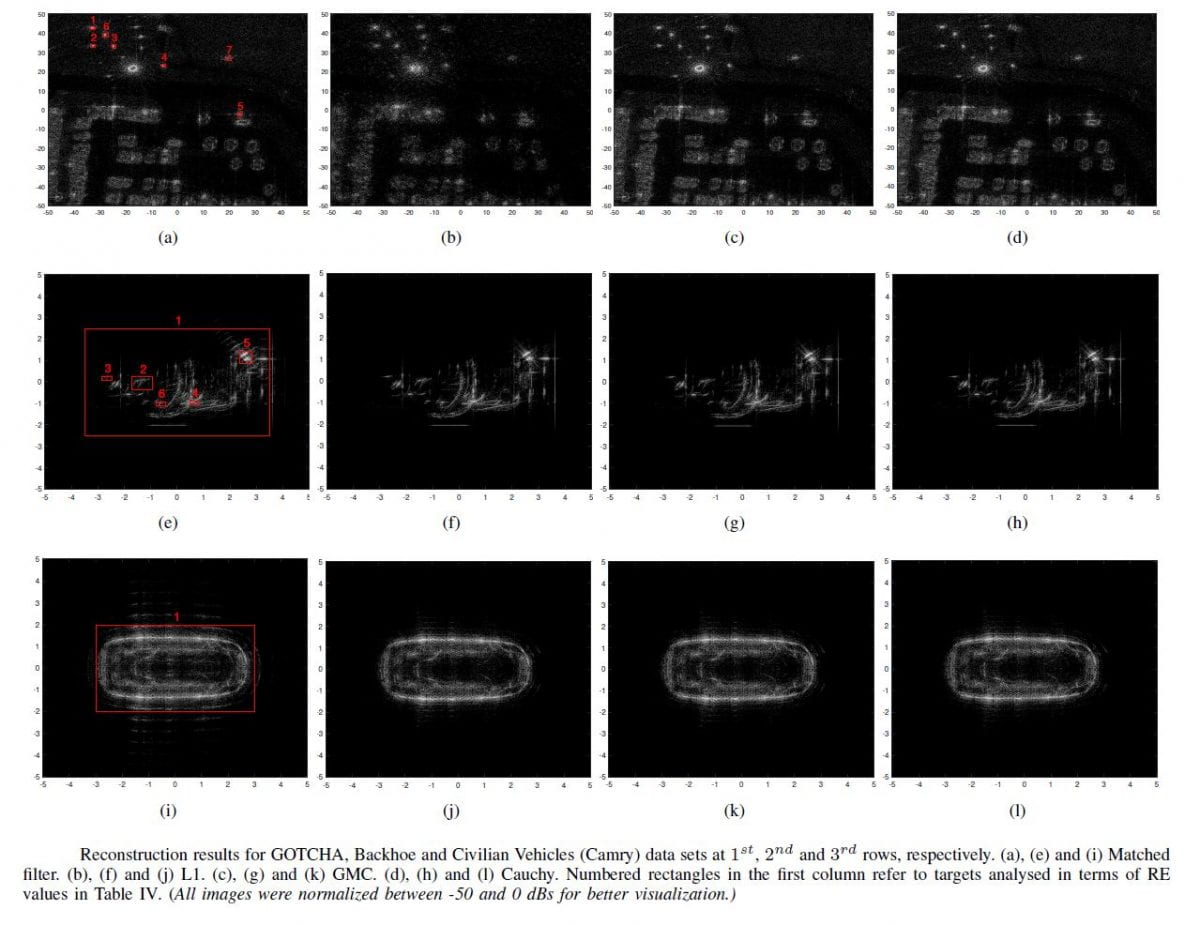
The proposed method is compared to several methods employing classical penalty functions such as total variation (TV) and L1 norms, and to the generalized minimax-concave (GMC) penalty. We show that the proposed Cauchy-based penalty function leads to better image reconstruction results when compared to the reference penalty functions for all SAR imaging inverse problems in this paper.
Super-resolution

Image Formation
De-speckling

Ship wake Detection

Further information
[1] Karakuş, O., & Achim, A. (2020). On solving SAR imaging inverse problems using nonconvex regularization with a Cauchy-based penalty. IEEE Transactions on Geoscience and Remote Sensing.
[2] O. Karakuş, I. Rizaev and A. Achim, “A Simulation Study to Evaluate the Performance of the Cauchy Proximal Operator in Despeckling SAR Images of the Sea Surface,” IGARSS 2020 – 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 2020, pp. 1568-1571, doi: 10.1109/IGARSS39084.2020.9323696.
Contact
Oktay Karakuş, Igor Rizaev, Alin Achim
Funding
This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) under grant EP/R009260/1 (AssenSAR).
